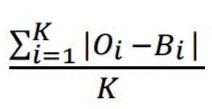Több mint egy éve tombol a világméretű pandémia. Mindenki élettere leszűkült, de vajon azok az adatok amiket látunk, mennyire lehetnek valósak? Ki tudja megmondani, hogy mit higgyünk el? A vírus terjedésével együtt terjednek az összeesküvés-elméletek, a különféle hamis és félrevezető tartalmak.
A bejegyzésem célja az, hogy mialapján szűrhetjük ki az álhíreket és választhatjuk ki egy ilyen lehetetlennek tűnő helyzetben a valós információkat az adott problémáról.
Sajnos nem vagyok túl jó matematikából, és vélhetően ezzel nagyon sokan vagyunk még így. Szerencsére viszont vannak akik kitűnőek a számok terén és így az ő tudásukra támaszkodhatunk. A bejegyzésem alapjául egy olyan matematikai törvény szolgál, amely azt mutatja meg, hogy a látszólag véletlen számok eloszlása egy adott, nagyon is szabályos mintát követ. Sokak számára felfoghatatlan, hogy egy véletlen eloszlás hogyan követhet egy bizonyos mintát, de mindez valóban így van. A fenti probléma vizsgálatához, vagyis a hírek és adatok valóságtartalmához ezt a törvényt úgy használhatjuk, hogy megtekintjük eltérés mértékét, nagyságát, amely rá fog világít arra, hogy vagy az adatok vagy helytelenek, hibásak, vagy manipuláltak. Mielőtt bárki is farkast és csalást kiáltana, a mérések eredménye nem feltétlenül magát a csalást jelzi, csupán az adatok helytelenségét. A statisztikai módszerek kiválóak arra, hogy megmutassák a normálistól való eltérést. A megfejtését ránk bízza, amivel nem biztos, hogy az általunk feltett kérdés válaszához közelebb kerülhetünk.
A cikk alapjául egy amerikai marketing-vezető, Kevin Basset munkája szolgál, aki statisztikai módon vizsgálta a koronavírus adatokat világszerte. Ő maga részt vett egy alkalmazás létrehozásában, amely megmutatja a világban terjedő vírust a publikus adatok alapján. (https://coronavirus.app/)
Tanulmányában első lépésként ismerteti a Benford-törvényt, ezért így teszek én is. Aki nem bírja a matekot nyugodtan átugorhatja, elegendő annyit tudni nagyon leegyszerűsítve, hogy ha bármennyi számot kiválasztunk és azoknak az első számjegyeiket megszámoljuk, akkor azok gyakrabban fognak 1-essel kezdődni, mint 9-cel.
Innentől kezdődik a matek, vagyis a Benford-törvény ismertetése

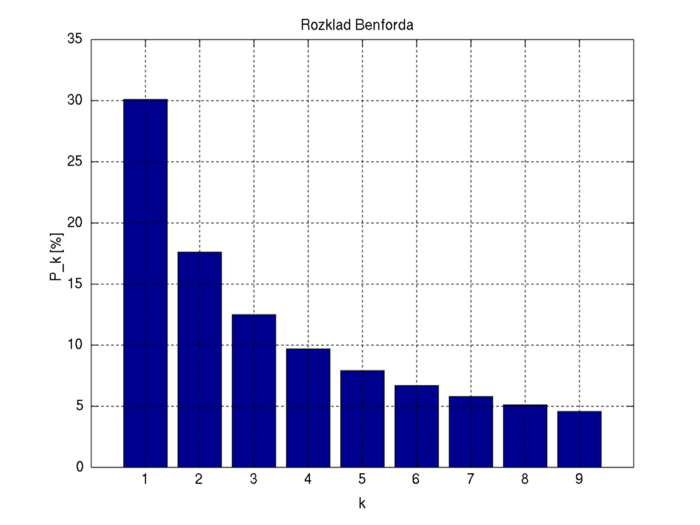
„Elsőként Simon Newcomb kanadai-amerikai asztrofizikus figyelte meg, hogy az egyetemi könyvtárban a logaritmus-táblázatok első oldalai erősebben elhasználódtak, mint az utolsók. Körülbelül 50 évvel később Frank Benford fizikus és mérnök is felfigyelt a jelenségre, és mivel az ő leírása alapján lett ismert, innen származik a Benford törvénye elnevezés. A hallgatók és oktatók az alacsonyabb számmal kezdődő táblázatokat használták többet. Rájött, hogy ha véletlen számokat veszünk számok bármely egyenletes eloszlású halmazából, akkor a számok gyakrabban fognak 1-gyel, mint 9-cel kezdődni. Bármilyen eredetű legyen is egy szám – pl. tavak felszíne, munkatársak lakásának házszáma, az egész számok négyzetgyökei – körülbelül hatszor olyan gyakran kezdődik 1-gyel, mint 9-cel. A számok kb. 31%-a kezdődik 1-gyel, 19%-a 2-vel, 12%-a 3-mal és a százalékok a számok nagyságával egyre csökkennek. Benford törvénye tehát csak a több számjegyű számok bal oldali első számjegyére vonatkozik.”
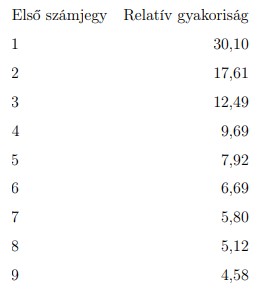
Azt a valószínűséget, amely azt mutatja, hogy egy szám az n számjeggyel kezdődik, a következő képlet jelzi előre, nagy pontossággal:
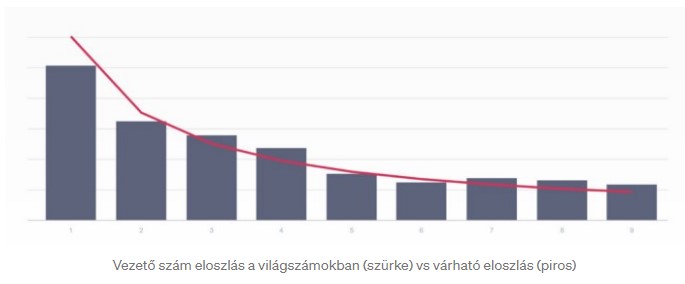
Benford törvénye a legtöbb dologra tökéletesen működik, ám vannak olyan estek amikor nem alkalmazható. Kiválóan megmutatja, ha valaki egy statisztikai adatot látszólag véletlen számokkal szeretne feltölteni, mint mondjuk egy adóbevallás, vagy egy eredménykimutatás. Azonban alkalmatlan ha példul emberek magasságára próbáljuk alkalmazni, mert míg az 1-es és 2-es számokra teljesülni fog a fenti törvény, addig nem sűrűen találkozunk 3 méteres emberekkel. Ha az adatok valóban véletlenek akkor egy ilyen grafikont kell kapnunk a kimutatott számokból.
Ami egy ilyen táblázatnak felel meg, viszont fontos megjegyezni, hogy ez a képlet csak tízes számrendszerben igaz.
A matekon túl
A fenti matek elmagyarázza ugyan az elméletet, de ettől még nem tudjuk, hogyan is lehet ezt használni. Sok cikk és városi legenda létezik, hogy az amerikai adóhivatal (ISR) használja a fenti képletet a csalások kiszűrésére, de ezt senki nem erősíti meg, bár nem is cáfolják. A magyar adóhivatal egy hallgató megkeresésére több éve azt a választ adta, hogy nem használja a törvényt a magyar adócsalók kiszűrésére. Térjünk hát vissza a koronavírus világméretű adatainak vizsgálatára. Itt elemezni fogjuk az egész világ számainak vezető adatait (= az egyes országok összege) az egyes napok kezdete óta (figyelembe véve az összesített eseteket, az új eseteket, a halmozott és az új halálozásokat).
Mit elemezzünk pontosan?
Kevin Basset cikkében kitér arr, hogy a következő lépés annak kiderítése, hogy pontosan milyen adathalmazokat kell elemeznünk. Az általuk fejlesztett alkalmazásban több begyűjtött adattal dolgoztak. Lényegében négy állt a rendelkezésükre:
- A – Napi új esetek
- B – Napi új halálesetek
- C – Napi összesített esetek
- D – Napi összesített halálozás
A fenti világdiagramon mind a négyet egyesítettük. De ebben a cikkben továbbhaladva (csakúgy, mint a Benford törvénytáblázatában, amelyet a Coronavirus App-on mutatunk be) az A-t B-vel és a C-t D-vel fogjuk csoportosítani. Minden országhoz két tesztet futtatunk. Ezek a tesztek megmondják: mennyire természetesek a kormányok által jelentett összesített számok? És mennyire természetesek a kormányok által jelentett új számok?
Önmagában a diagram meglehetősen valós képet ad arról, hogy az elosztás valamilyen módon Benford törvényét követi-e vagy sem. De ahhoz, hogy megközelítésünk matematikailag megalapozott legyen, be kell vezetnünk egy átlagos abszolút eltérés (MAD) nevű mértéket .
MAD lényegében számszerűsíti, mekkora az eltérés Benford-törvénytől. Minél alacsonyabb a MAD, annál természetesebbnek tűnik az eloszlás. Minél nagyobb a MAD, annál valószínűbb az adatokkal valamilyen probléma van.
A fenti képletből a K-val a kezdeti számjegyek számát jelöli. Valójában mindez nagyon egyszerű. Számítsuk ki minden egyes számjegyre (1–9) a megfigyelt eloszlást (O) és a Benford által megjósolt különbség (B) * különbségét. A MAD egyszerűen ennek a 9 értéknek az átlaga. Az eredménynek abszolút (tehát pozitív) számnak kell lennie. Ellenkező esetben a negatív értékek törlik a negatív értékeket, és a MAD mindig 0.
Az eredmény
Sok szó és matek után nézzük meg, hogy a gyakorlatban milyen adatokat látunk. Az eredeti cikk írója a tanulmány megjelenésekor 113 ország adatai alapján megvizsgálta a 10 legjobban megközelítő országot, valamint a 10 legrosszabb MAD mutatóval rendelkező országot. Mi inkább most a saját szemszögünkből vizsgálunk meg pár országot. Nézzük először a legfertőzőbb országok közé tartozó USA elemzését.
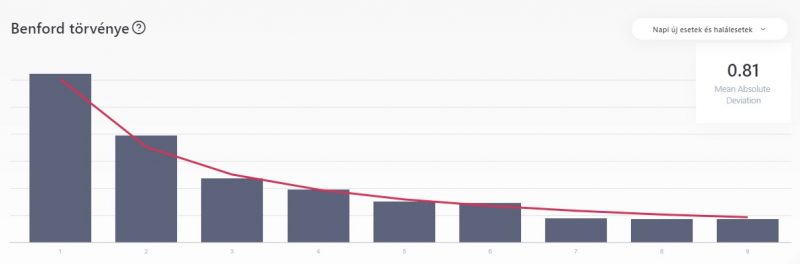 USA a 2021. március 15-i adatai alapján. Látszik, hogy a MAD mutató az elfogadható 0.81 értéket mutatja, tehát nagyon megközelíti a Benford-törvény ideális görbéjét. (30 081 605 igazolt eset)
USA a 2021. március 15-i adatai alapján. Látszik, hogy a MAD mutató az elfogadható 0.81 értéket mutatja, tehát nagyon megközelíti a Benford-törvény ideális görbéjét. (30 081 605 igazolt eset)
Most nézzük meg Olaszország adatait
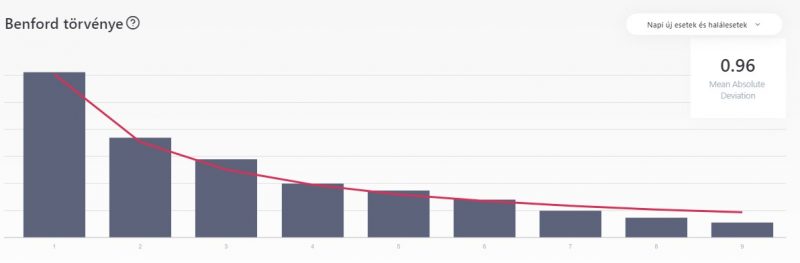
Itt is a 2021. március 15-i adatokat láthatjuk (3 223 142 igazolt eset)
A következő ország legyen Ausztria, mivel sokszor emlegetik, hogy valamilyen formában őket követjük a védekezés terén
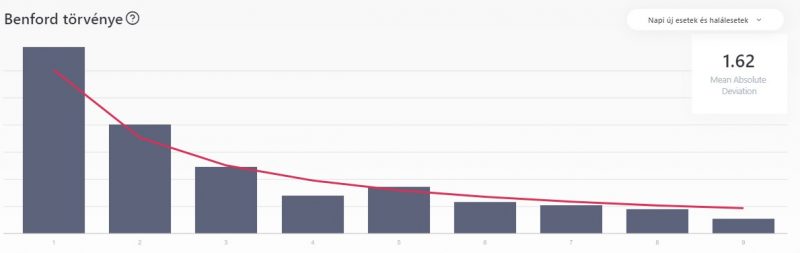 Ausztria is a 2021. március 15-i adatokat mutatja, de itt már megmutatkozik a napi adatokban a MAD növekedése. (495 464 igazolt eset)
Ausztria is a 2021. március 15-i adatokat mutatja, de itt már megmutatkozik a napi adatokban a MAD növekedése. (495 464 igazolt eset)
Most pedig nézzük meg Magyarországot
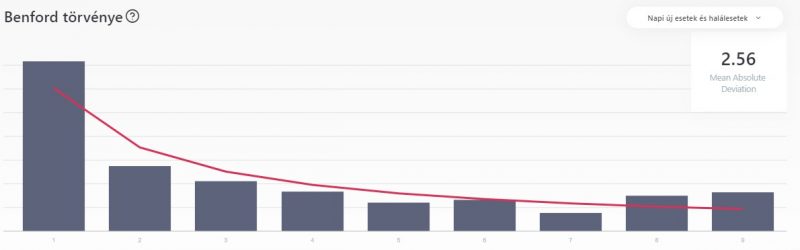 Ebben az esetben is a 2021. március 15-i adatokat mutatja a grafikon (524 196 összes igazolt eset)
Ebben az esetben is a 2021. március 15-i adatokat mutatja a grafikon (524 196 összes igazolt eset)
Itt már jóval nagyobb MAD-szám látszik. Sokan kiálthatnak most csalást, illetve hogy manipulálják az adatokat, viszont azt is fontos megjegyezni, hogy a pontatlanság mértéke még mindig nem emeli a MAD alapján Magyarországot a 10 legnagyobb eltérést mutató ország közé, amelyek a 8-14-es tartományban mozognak. Jól látszik viszont az, hogy azokban az országokban, ahol a tesztelés sokkal nagyobb méreteket ölt, ott a MAD mértéke is kisebb.
Végszó
A bejegyzésem némileg eltér a megszokott bejegyzéseimtől, bár ettől függetlenül sem célja semmilyen politikai véleménynyilvánítás, pusztán az adatelemzés segítségével rávilágítani arra, hogyan tudjuk kiszűrni a hamis tartalmakat. A nagyobb MAD szám rávilágít, hogy a számolás módja, vagy maguk a rendszerbe került adatok nem megfelelően oszlanak el. A Benford-törvényt felhasználták a Trump választások kielemzésére is, valamint több olyan HOAX is terjed az interneten, amely a fenti algoritmussal igyekszik igazolni, hogy a Biden szavazatokkal is csaltak. Ez utóbbit viszont ezt több nyilvános adat segítségével már megcáfolták. Ezért is fontos megjegyzeni, hogy nem a csalást mutathatja meg Benford törvénye, hanem azt is, ha valahol hiba van adatokban. De milyen hibák lehetnek például a fenti adatokban? Az igazolt esetek számolásának módja, a nem COVID-osnak számolt betegek, azok akik tesztelés nélkül átestek a betegségen, vagy fertőznek. Sok dolog befolyásolhatja az adott mérést, ezért semmiképpen sem lehet csalásnak nevezni a pontatlanságot.
Amennyiben kíváncsi vagy további országok adataira: https://coronavirus.app (A kiválasztott ország adatainak végén található a Benford-diagram.)
Források:
- https://hu.wikipedia.org/wiki/A_sz%C3%A1mok_haszn%C3%A1lat%C3%A1nak_gyakoris%C3%A1ga
- https://en.wikipedia.org/wiki/Benford%27s_law
- https://kevinbasset.medium.com/i-used-benfords-law-to-analyze-covid-19-in-113-countries-1a1194668069